Case Number : Case 1495- 17 March Posted By: Guest
Please read the clinical history and view the images by clicking on them before you proffer your diagnosis.
Submitted Date :
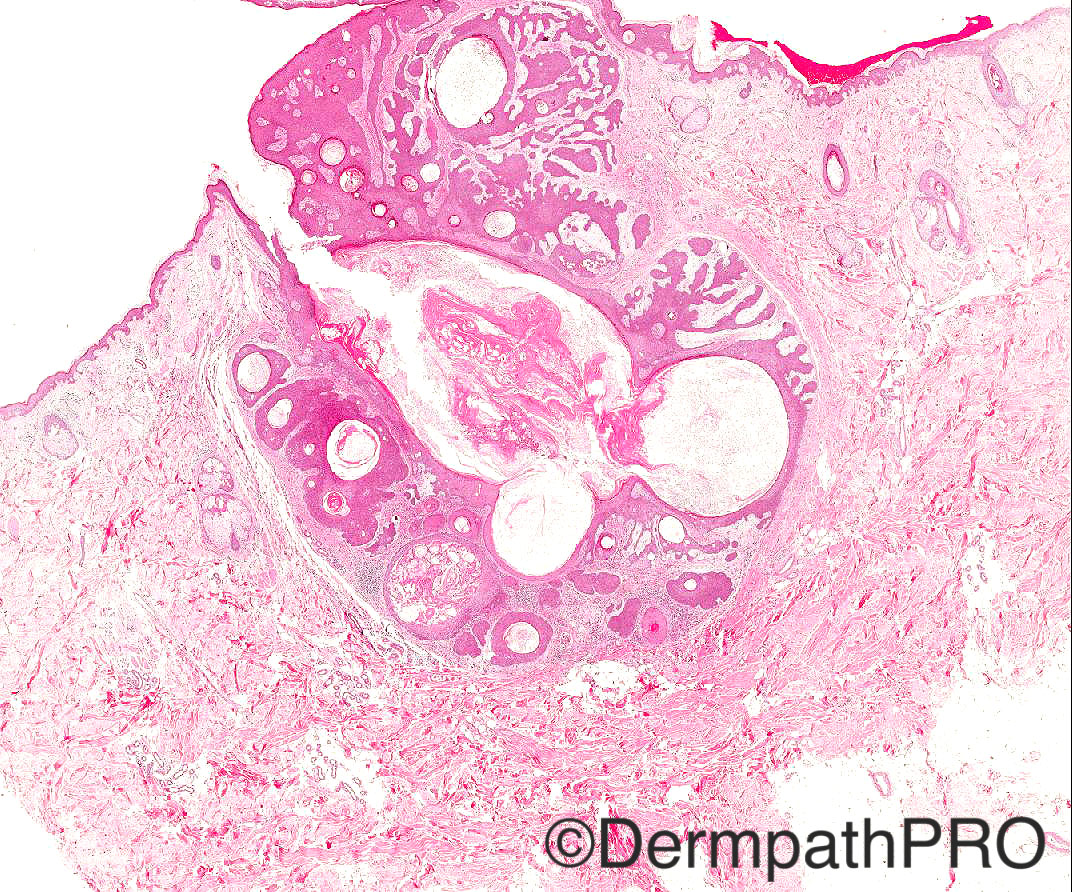
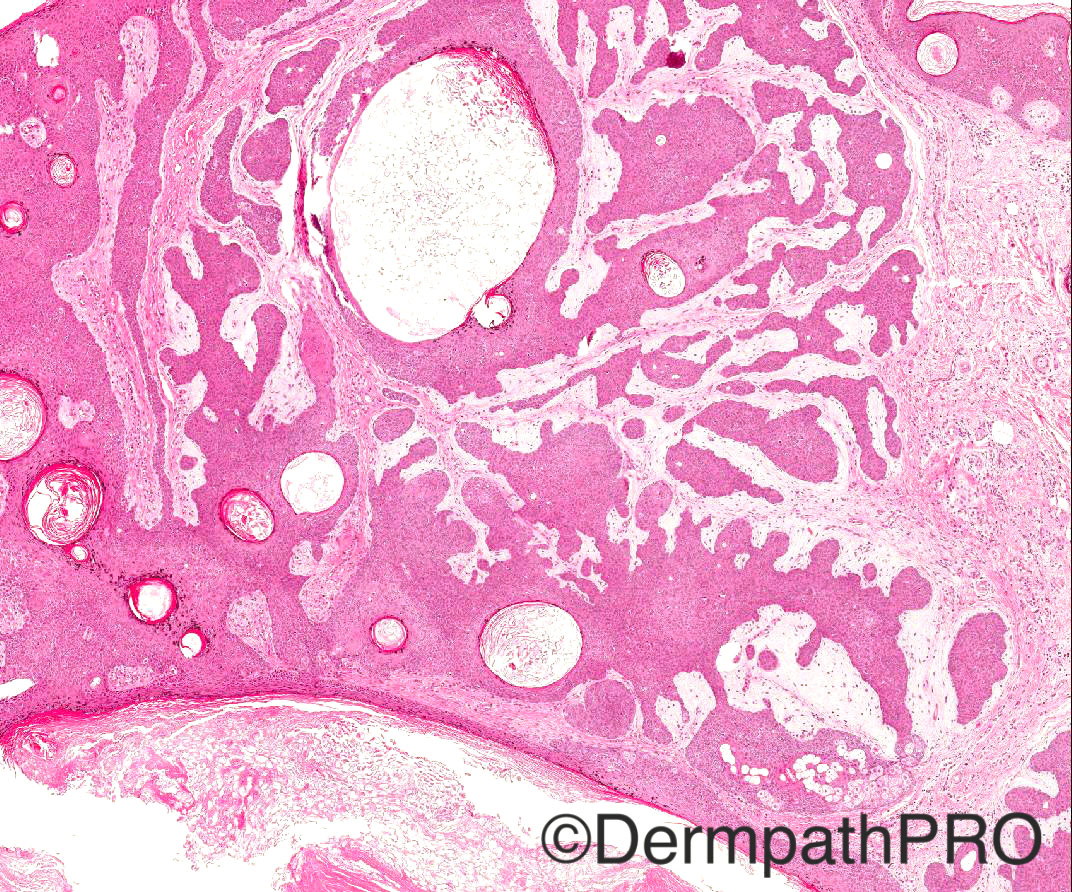
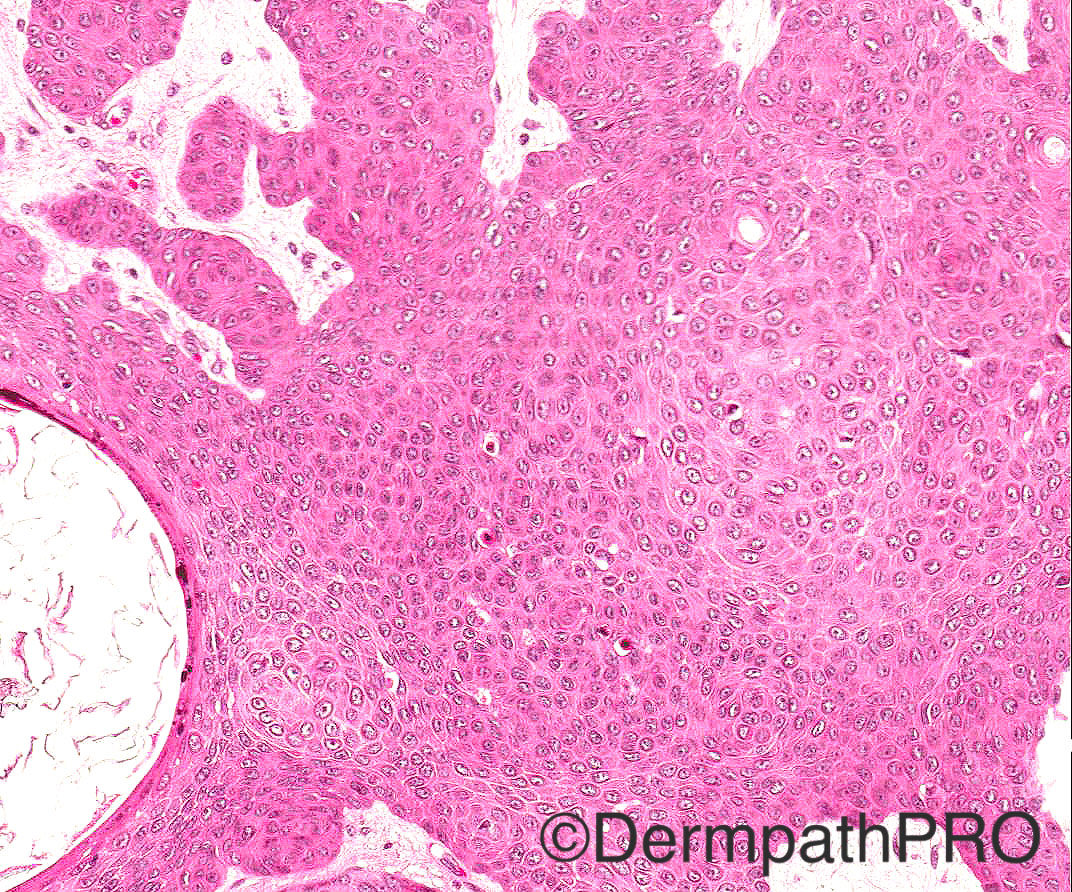
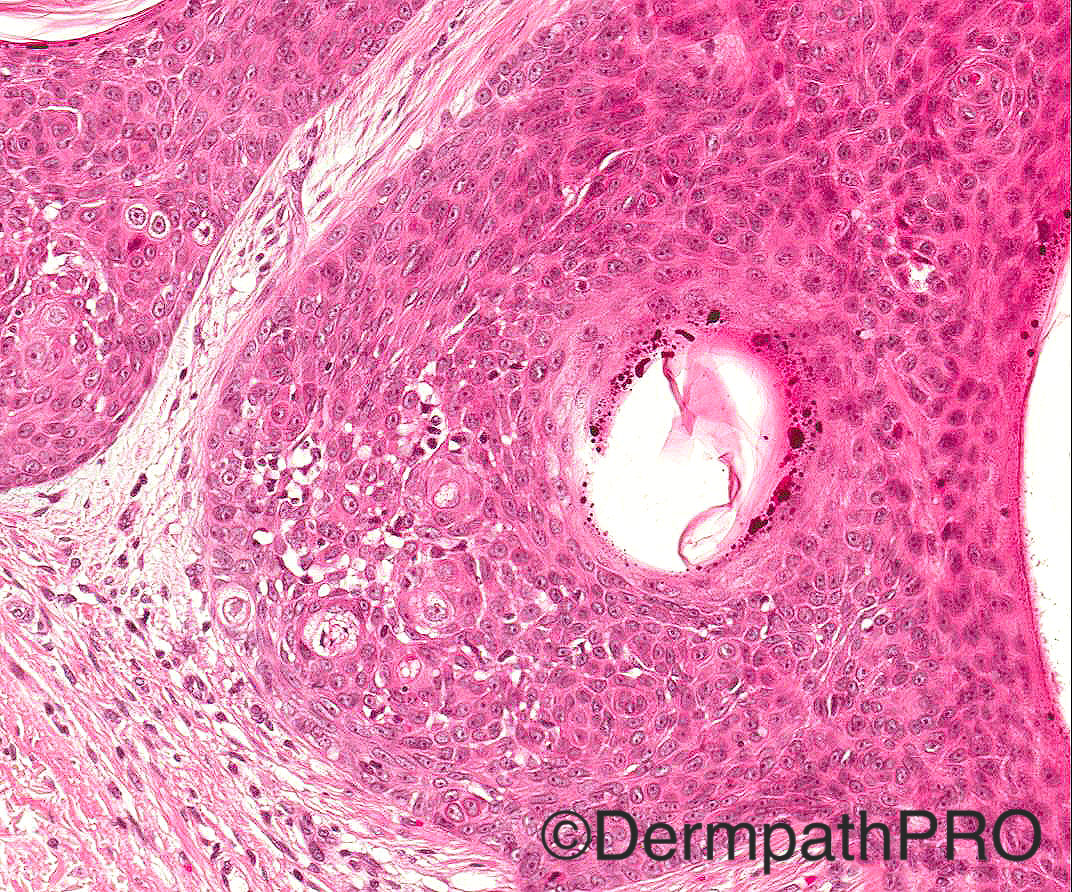
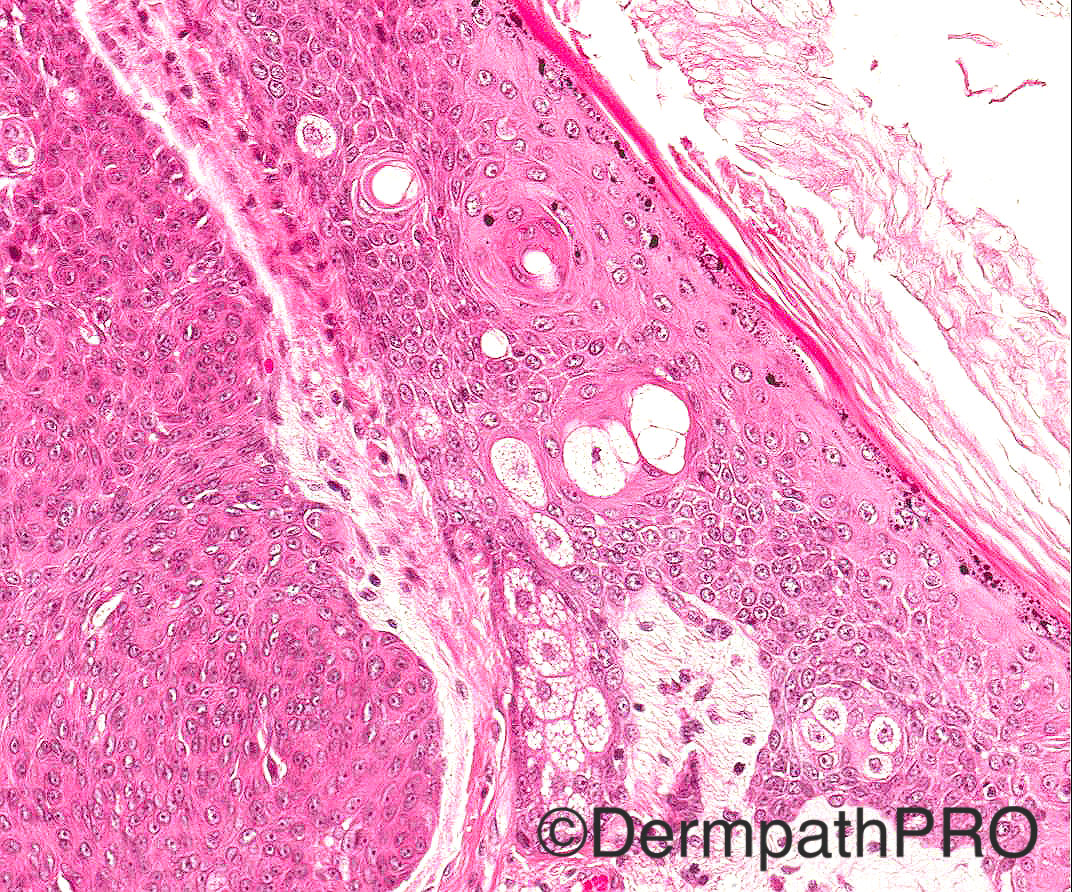
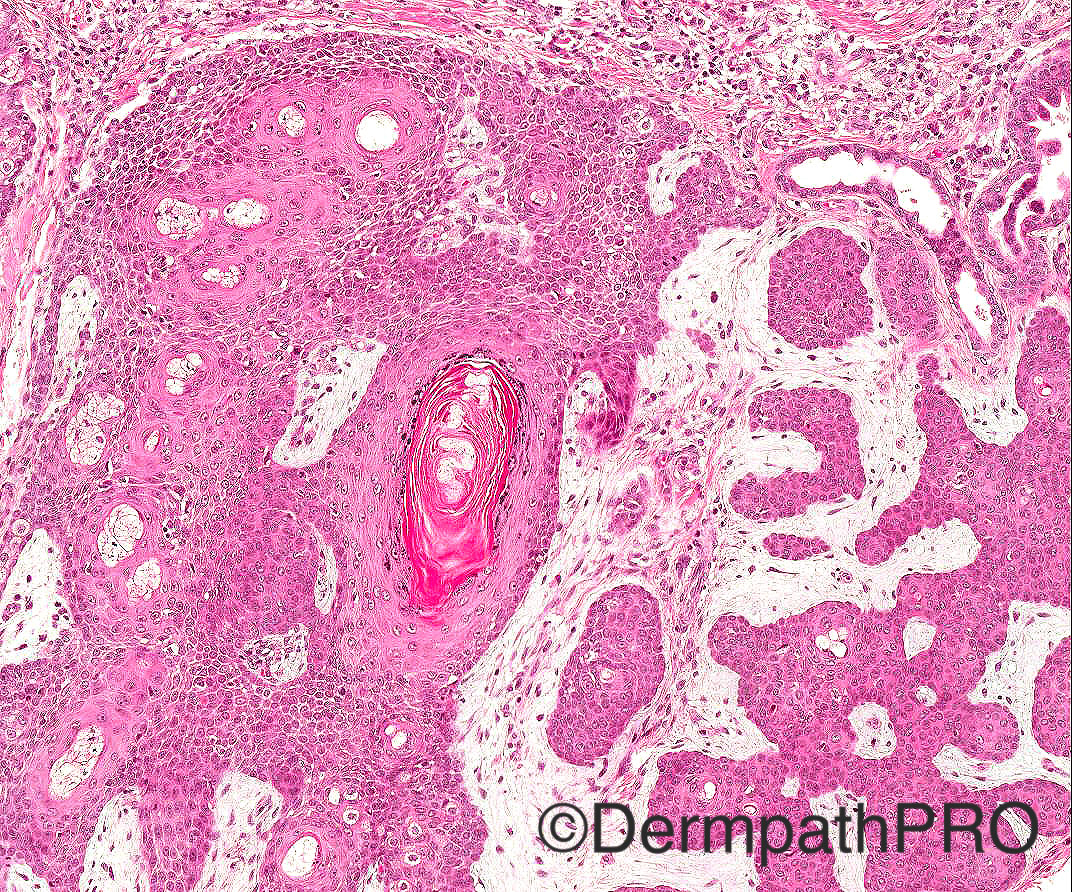
60/M odd cystic lesion face
Case posted by Dr Arti Bakshi
Case posted by Dr Arti Bakshi

Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.