Case Number : Case 2661 - 17 September 2020 Posted By: Saleem Taibjee
Please read the clinical history and view the images by clicking on them before you proffer your diagnosis.
Submitted Date :
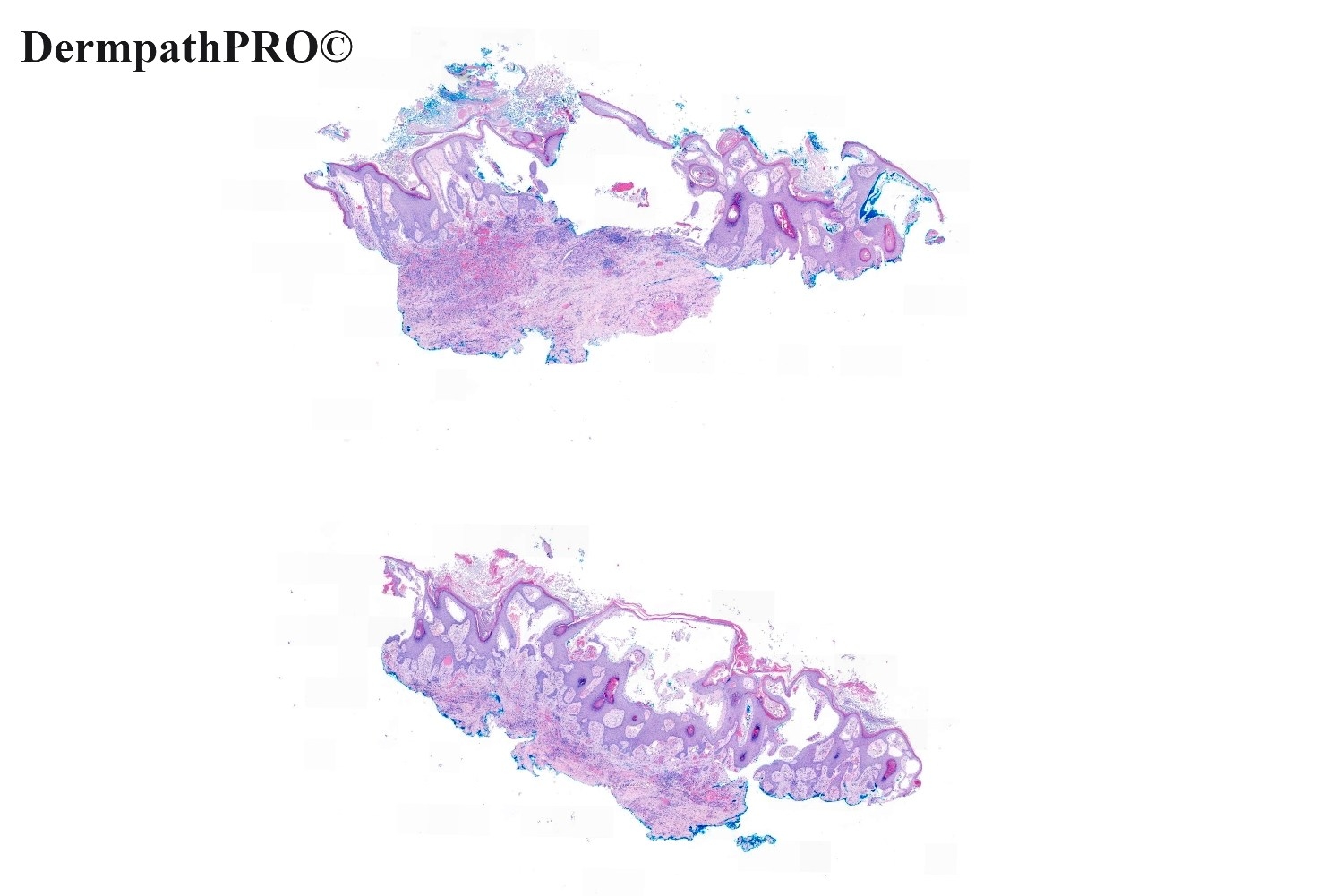
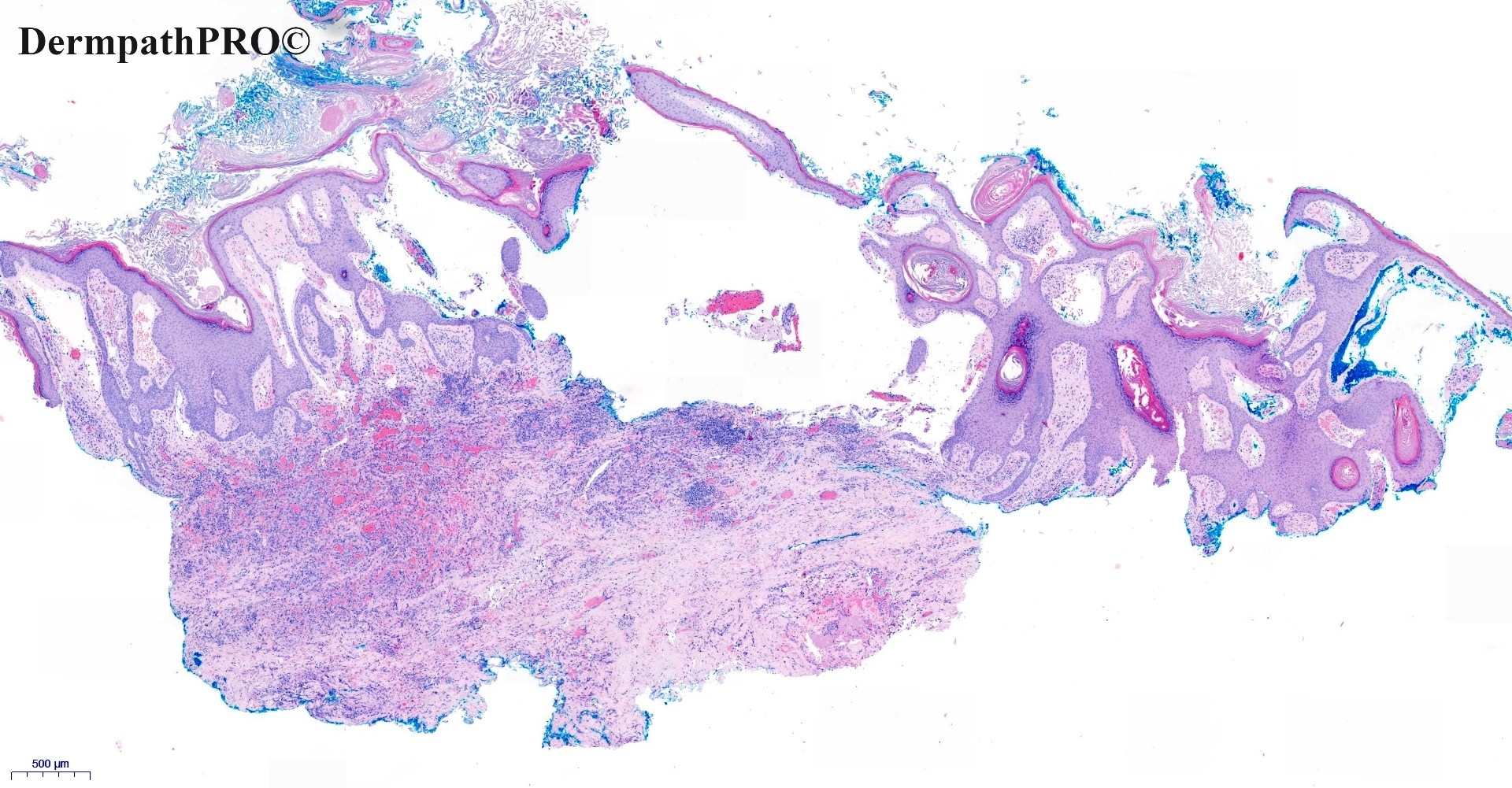
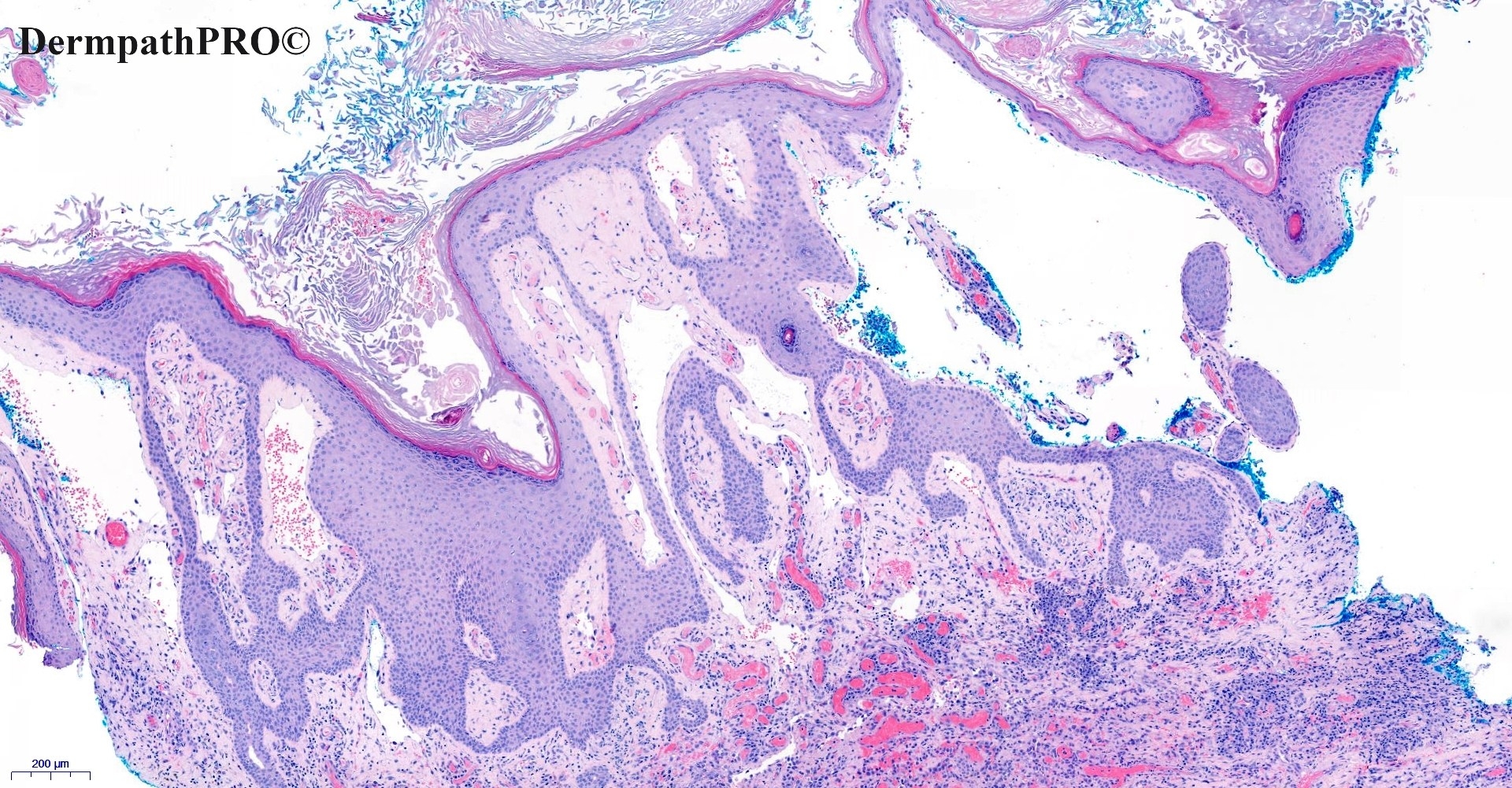
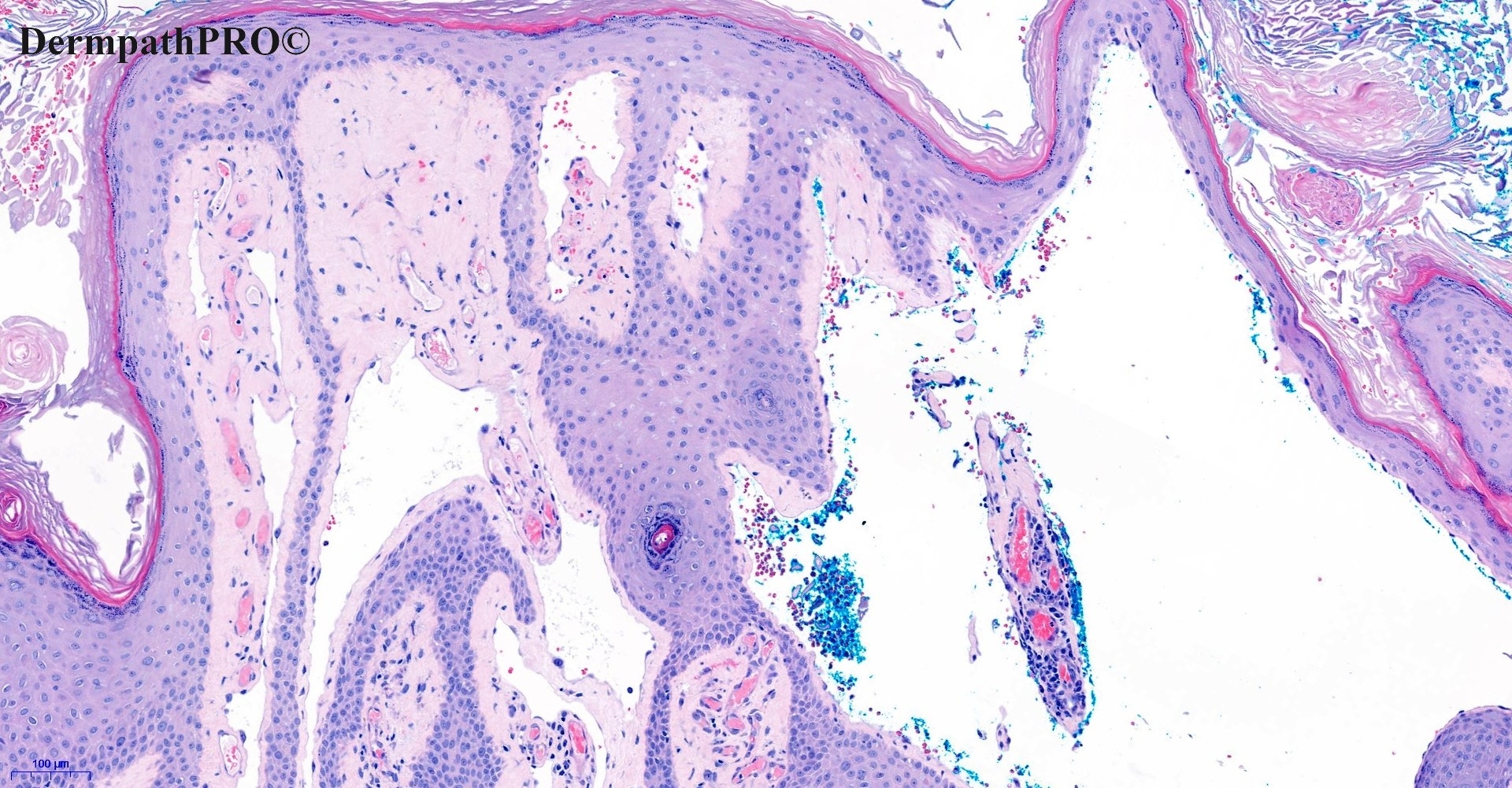
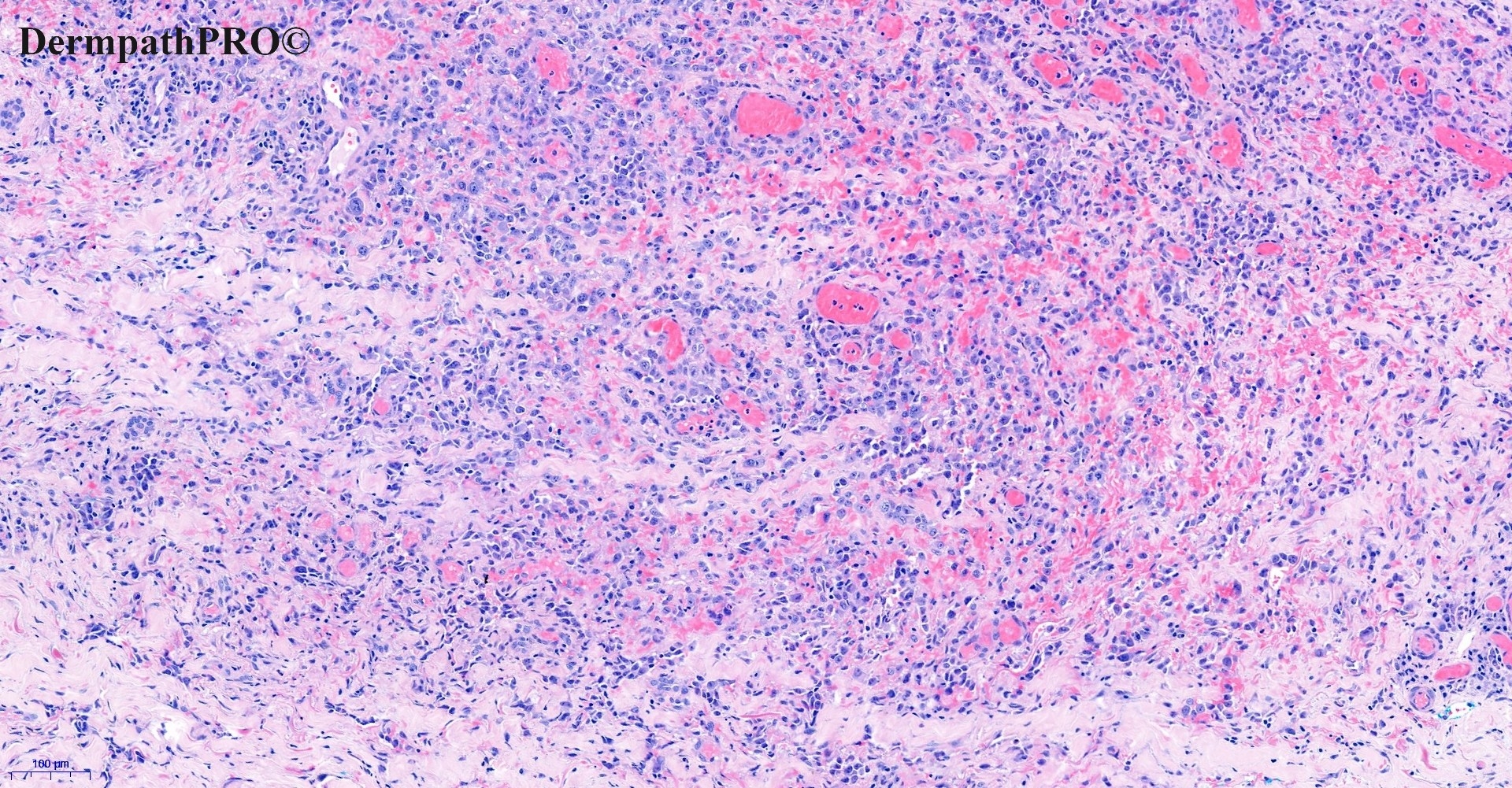
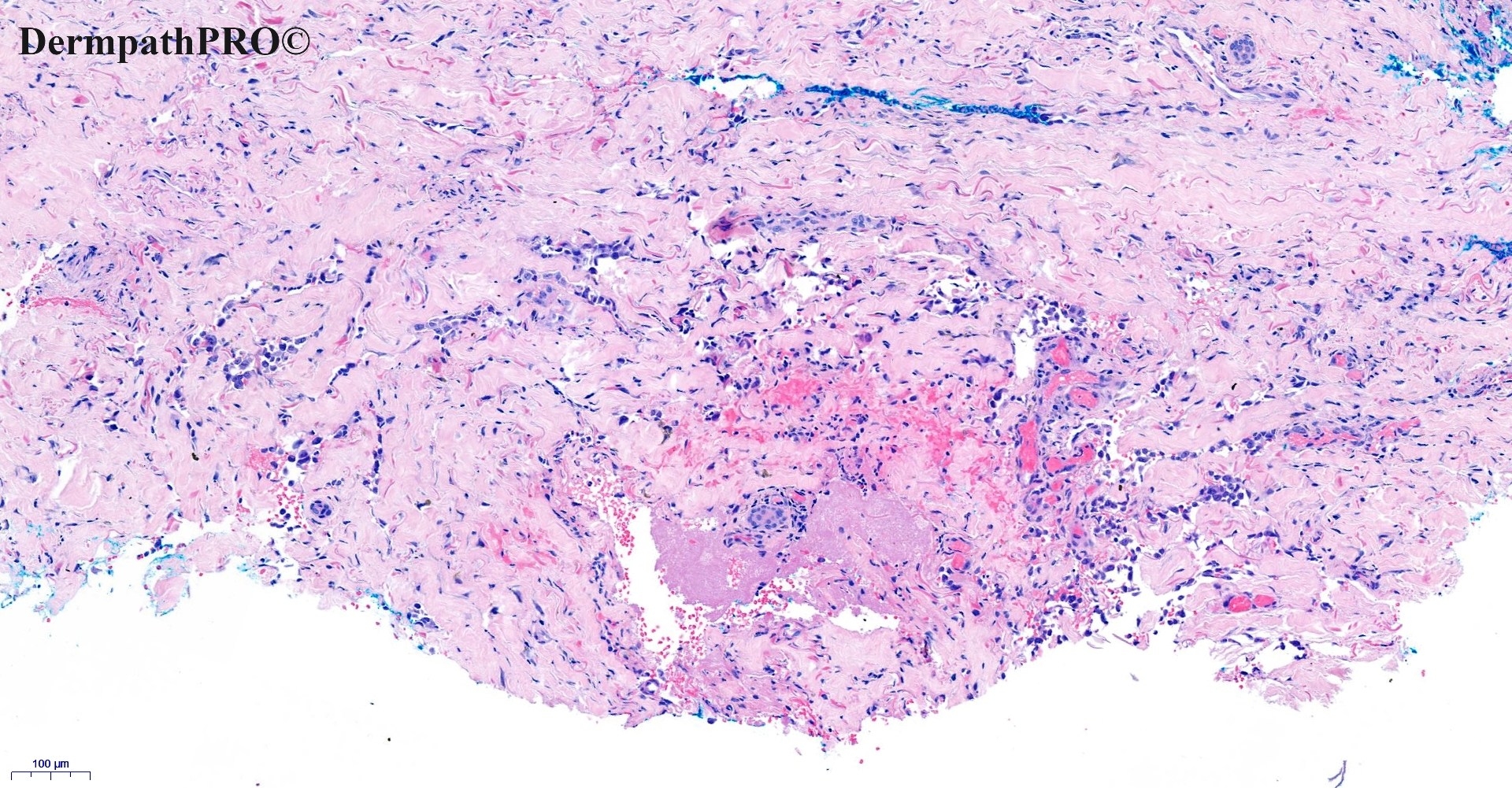
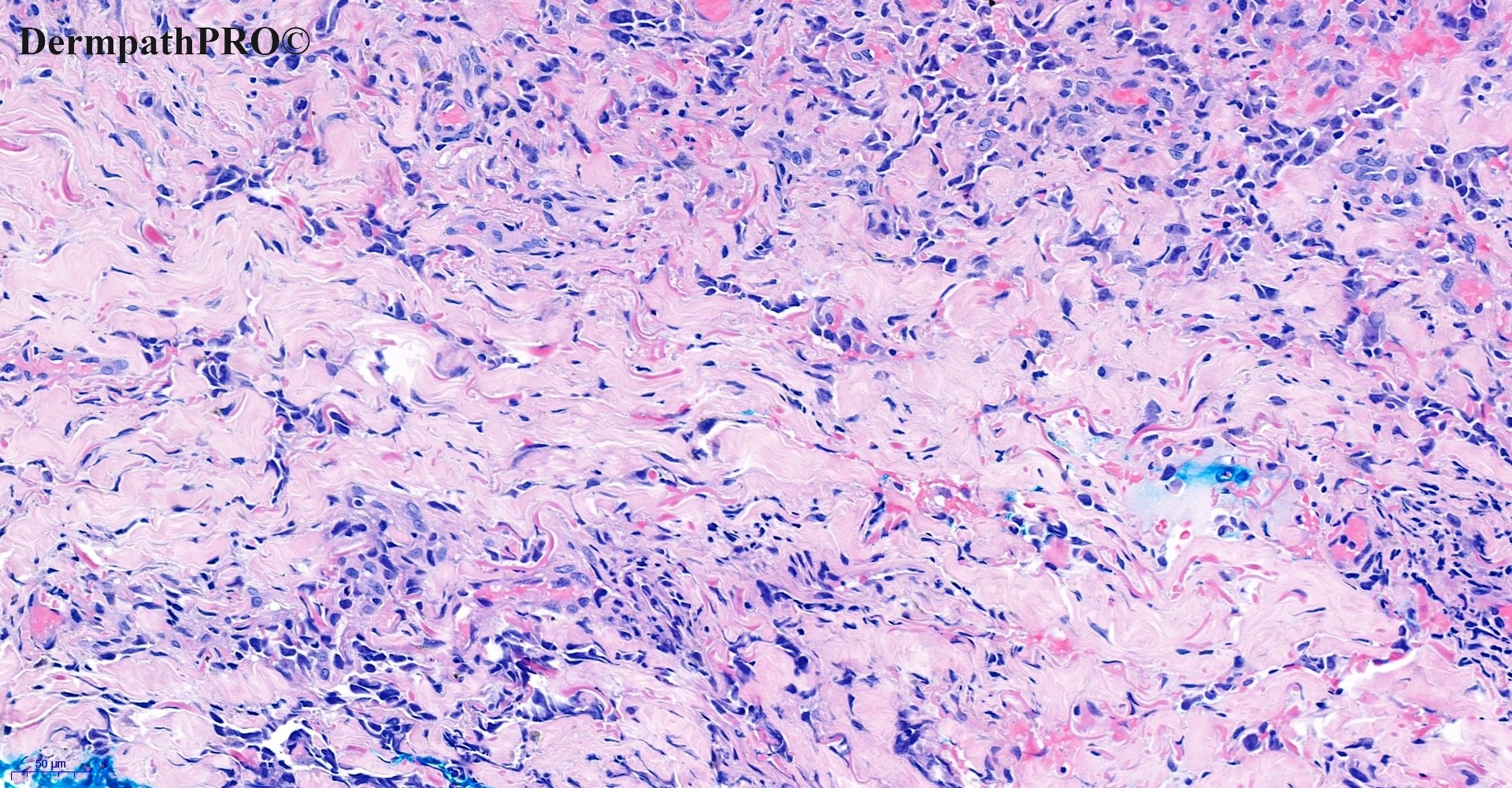
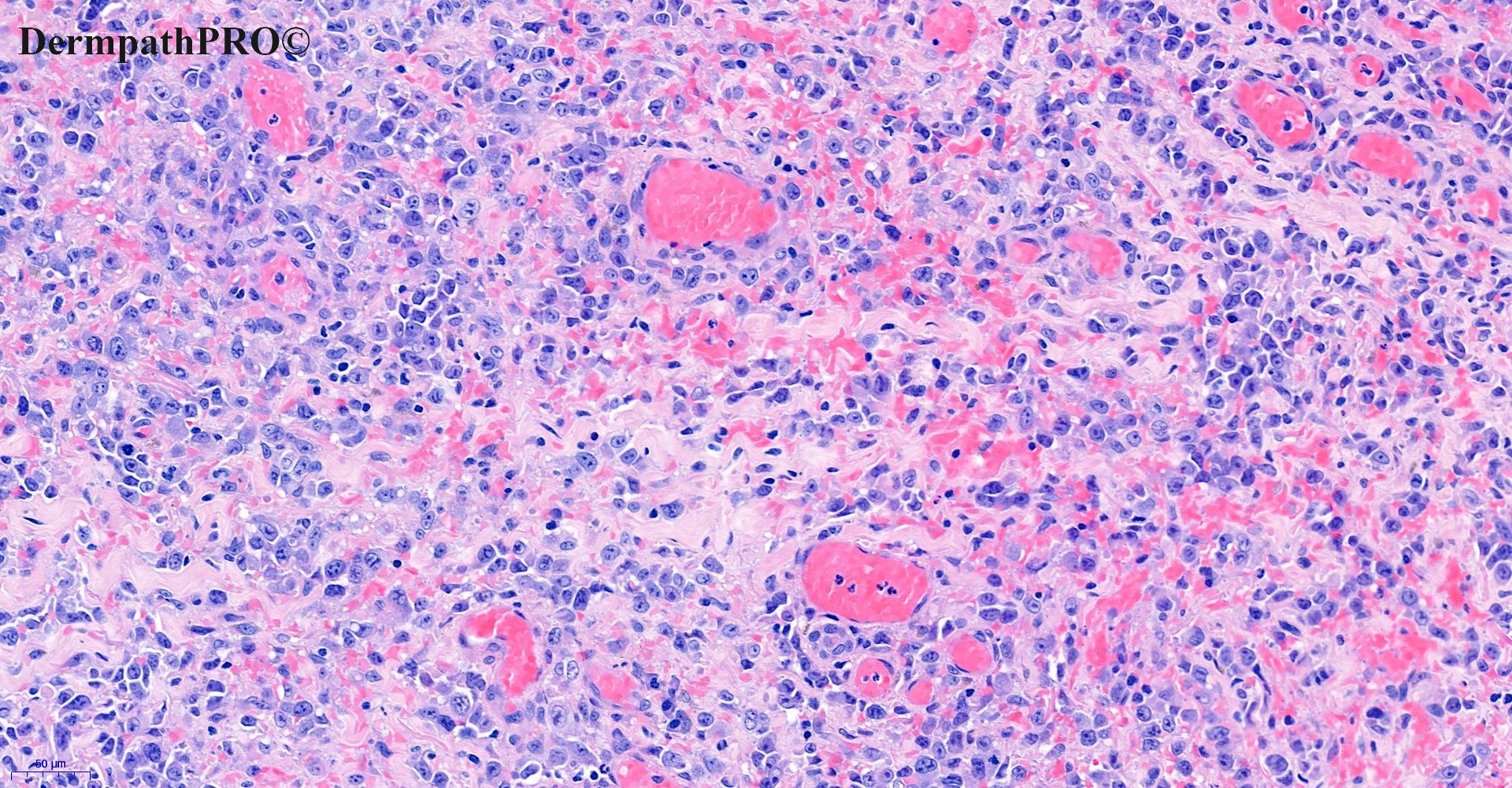
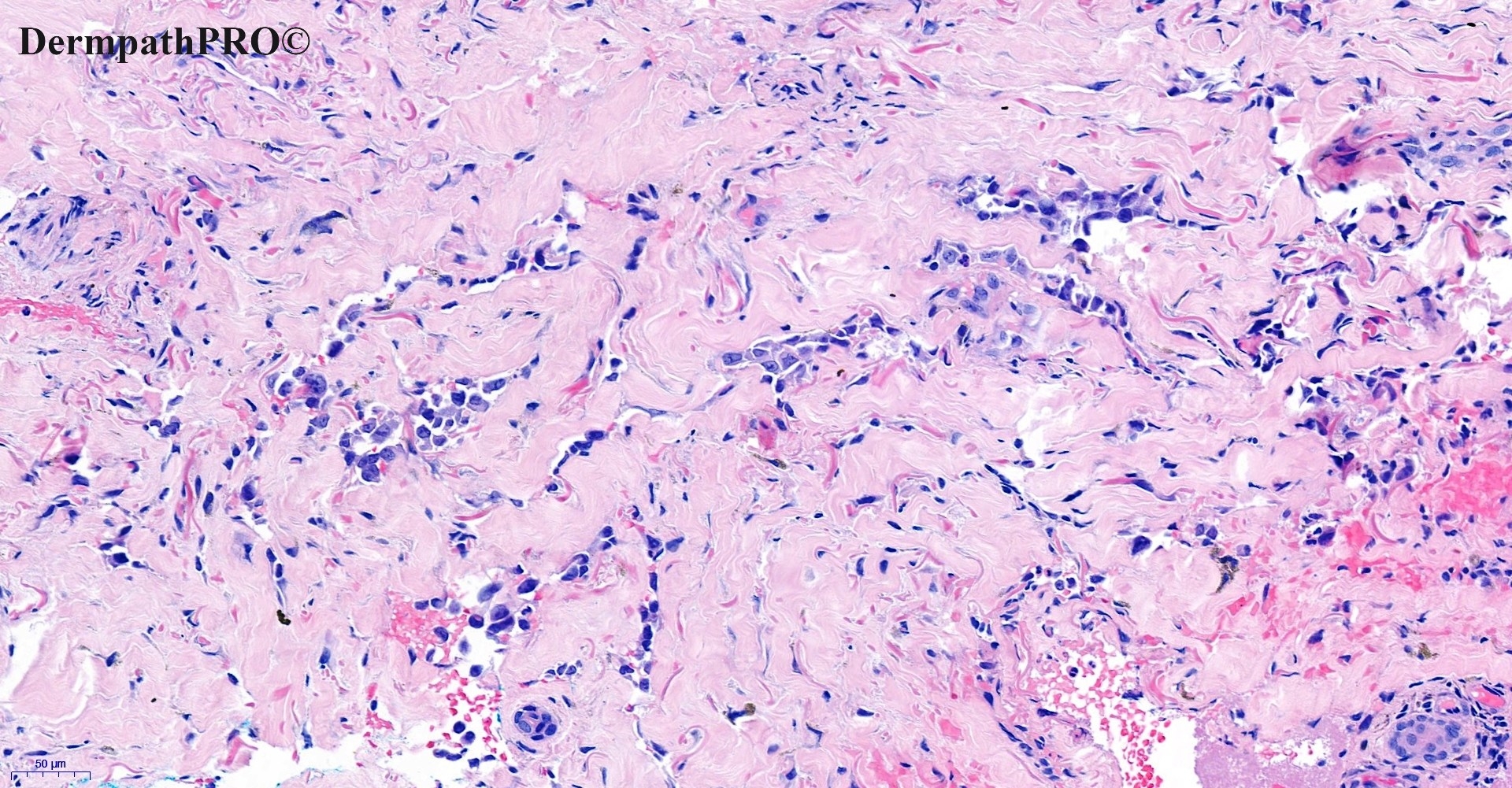
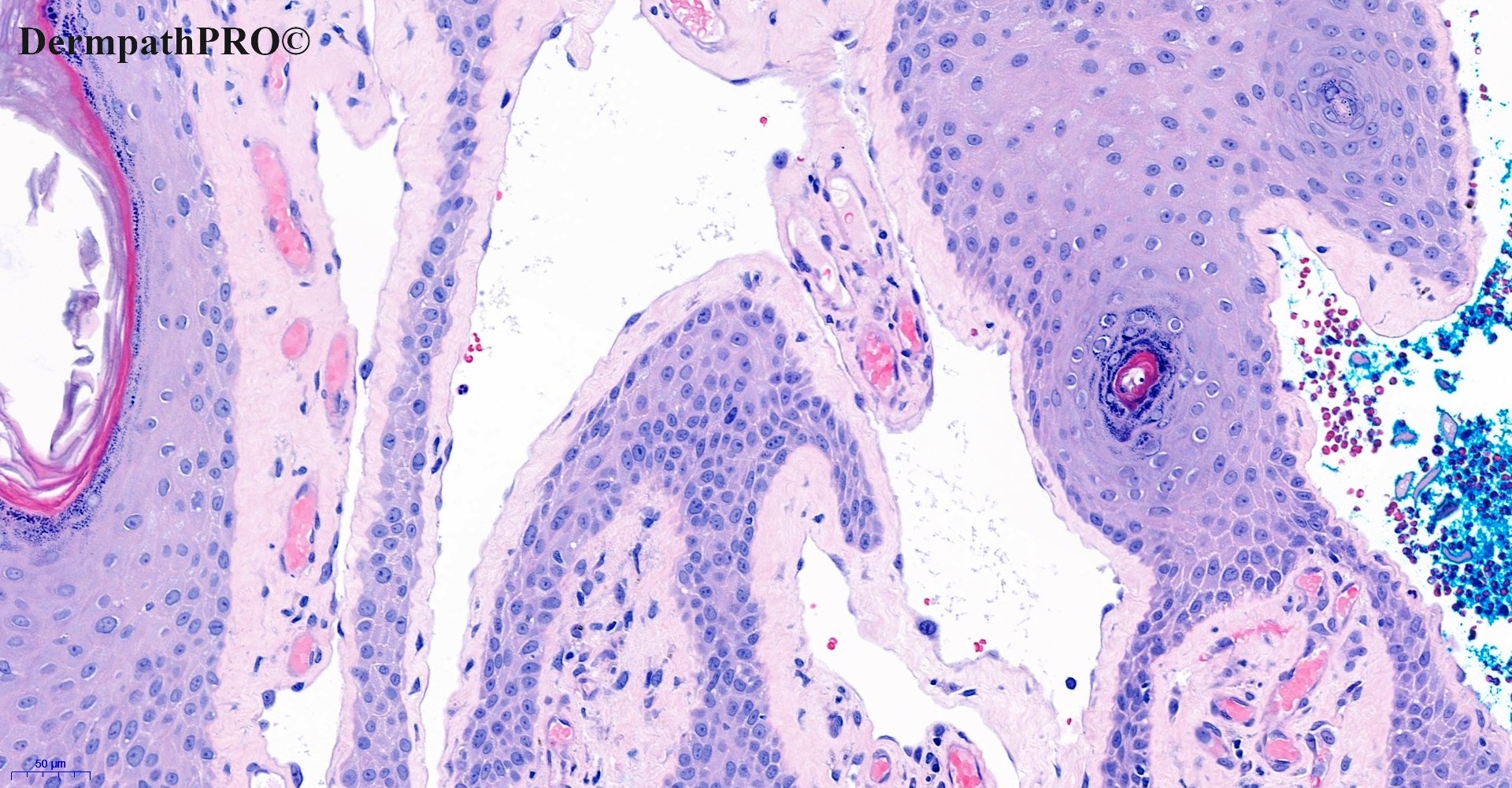
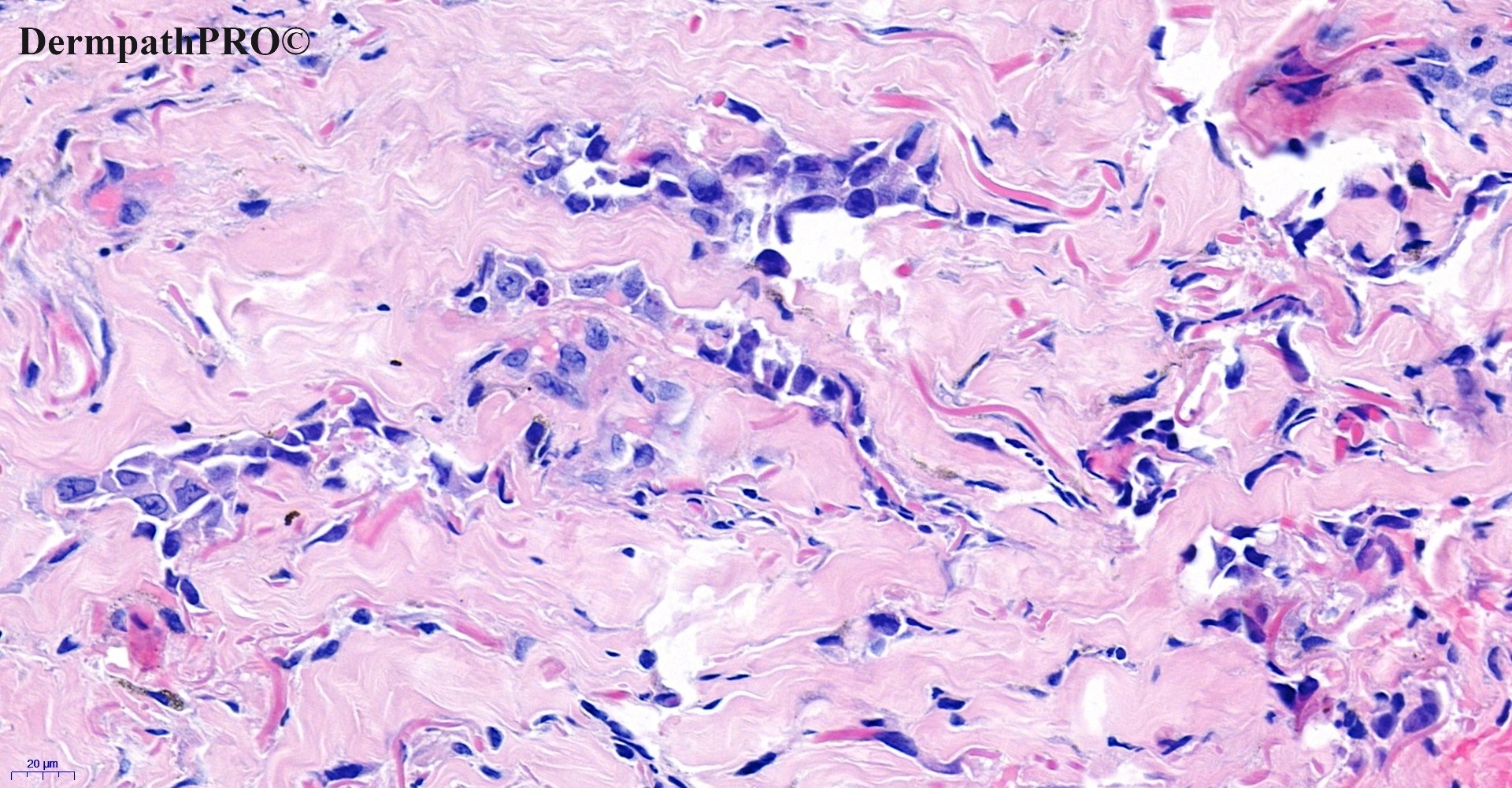
83M, left leg.

Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.